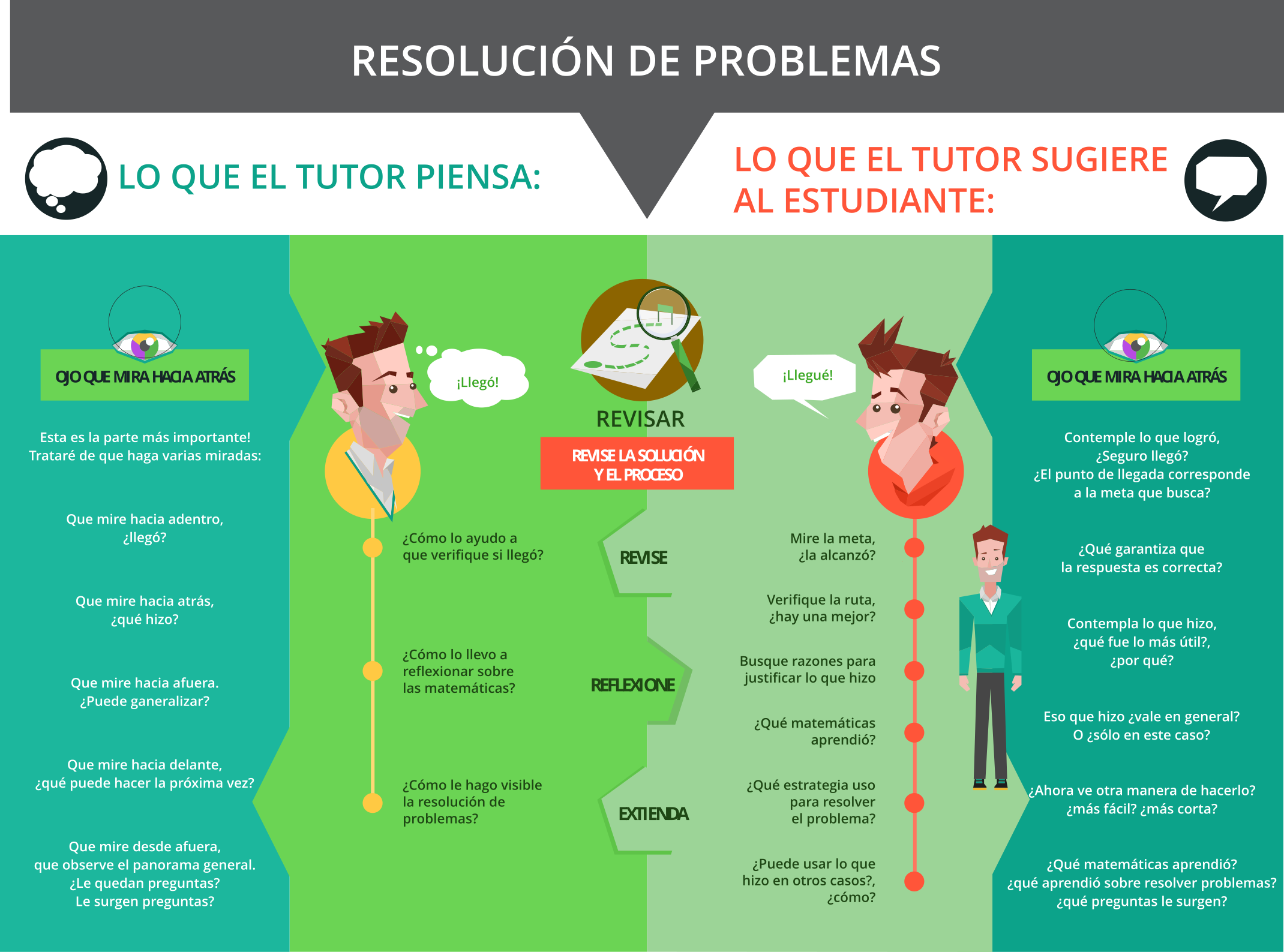
Verificar la solución
Al finalizar, se debe
verificar el resultado
y reflexionar sobre el
proceso para
llegar a este.
Al finalizar, se debe
verificar el resultado
y reflexionar sobre el
proceso para
llegar a este.

 |
Arriésguese a hacer conjeturas sobre cuál es el problema del estudiante, qué está pensando, qué le motiva o qué siente. Impulse al estudiante a que se arriesgue, a que planteé conjeturas o ensaye caminos, pero controlando el rumbo, para no perder de vista la meta final, ni desviarse de ella. Atrévase a empezar y persevere, a pesar de cualquier dificultad. |
 |
Creer que uno lo sabe todo no solamente es pretencioso, es perjudicial para el aprendizaje. Cuando no sepa algo, reconózcalo, dígale al estudiante que va a averiguarlo o búsquenlo juntos. Y cuando se equivoque, sea sincero con el estudiante, no solamente logrará empatía con él, sino tendrá una oportunidad para que identifiquen el error y aprendan juntos. |
Pida que el estudiante verbalice lo que genera el problema. Es decir, busque que haga explicito el conocimiento tácito acerca del problema y qué es lo que no lo deja comenzar.
Piense en un ejemplo, en un caso particular.
Si el problema se resuelve en un solo paso, de manera directa, entonces llegó a su más simple expresión. Pero si hay más de un asunto por resolver, es conveniente que los separe.
 |
El estudiante es el actor protagónico. ¡Es él quien debe resolver el problema! Su principal rol es pensar activa y críticamente y comunicarlo. Debe relacionar lo que sabe con la nueva situación para encontrar un camino. Mantener los ojos en la meta y al final, una vez verifique que llegó al puerto y que el camino es correcto, debe reflexionar sobre lo hecho, para sacar provecho de la experiencia, avanzar en su comprensión de las matemáticas y fortalecer sus competencias de resolutor de problemas. |
 |
Apoyar al estudiante en el proceso, para que él comprenda el problema, encuentre un camino, llegue a una solución, y luego, lo más importante, reflexione sobre lo que hizo, para que aprenda matemáticas y a resolver problemas. El tutor es como la conciencia externa del estudiante, que lo hace caer en cuenta de manera sutil de sus problemas y éxitos. Se mantiene atento, le refuerza lo que hace, lo empuja para que persevere, pero se abstiene de pensar por él. Cuando el tutor no sabe, o se equivoca, lo reconoce. El tutor pregunta, escucha activamente, deja trabajar al estudiante sin presionarlo, analiza lo que él hace, y formula la siguiente pregunta. Trata de intuir si hay factores diferentes a los conocimientos, que están obstaculizando el trabajo y trata de ayudarlo a superarlos. |
 |
Resolver problemas es una competencia compleja que engloba muchas habilidades tales como: explorar, razonar, estimar, conjeturar, testear, explicar y probar, entre otras. Es un proceso activo de pensamiento que requiere ir más allá de lo que se conoce, pensar críticamente, extender las ideas o hacer síntesis. Para aprender matemáticas y aprender a resolver problemas a través de la resolución de problemas es necesario mantener una actitud consiente durante el proceso: comprender qué se tiene y qué se busca, identificar una ruta y seguirla sin perder de vista la meta, perseverar a pesar de los obstáculos, ser consciente de lo que hace mientras lo hace, y una vez se llega a una solución, reflexionar sobre lo que hizo y cómo lo hizo. |
 |
En matemáticas se resuelven problemas no con el fin de obtener “la respuesta”. Esta normalmente es irrelevante, pero el estudiante debe llegar a la respuesta correcta, por un camino correcto. Se resuelven problemas en matemáticas con el fin de aprender matemáticas: fortalecer la comprensión de los conceptos, relacionar diferentes conocimientos de matemáticas, generalizarlos o aplicarlos a otras disciplinas o a situaciones de la vida diaria, autoevaluar o evaluar externamente la comprensión de los conceptos o el desarrollo de ciertas competencias y en particular, ejercitar la competencia de resolver problemas. Un estudiante tiene éxito resolviendo un problema si comprende un concepto, si halla nuevas conexiones, si es consiente y supera una concepción errada o si comprende qué es lo que no comprende; así no haya llegado a la “solución” del problema. |
 |
Es una situación retadora, pero no imposible de resolver, ante la cual el resolutor no “ve” inmediatamente ni la respuesta, ni un único camino para solucionarla, pero está dentro de sus posibilidades diseñar una estrategia para llegar a la solución. Se diferencia de un ejercicio en que, en este último caso, el objetivo regularmente es reforzar una habilidad y sólo se requiere seguir un procedimiento establecido. Una misma situación puede ser un ejercicio para alguien y un problema para otra persona. Un buen problema reta al resolutor, mantiene su interés y le permite aprender en el proceso de solución. Tiene distintas soluciones y diferentes caminos para llegar a ellas. |
 |
La solución de problemas es un proceso de adivinación consiente. El error es un indicador de que hemos validado un camino incorrecto para llegar a la solución, y de ello aprendemos más que del acierto. Dele al estudiante la confianza y el ambiente seguro que le permita equivocarse, identificar por qué, reflexionar y seguir adelante. |
 |
Preguntar al estudiante es la mejor herramienta que tiene para ayudarle a aprender. Con preguntas logrará que cuestione sus razonamientos, proponga alternativas, encuentre errores y generalice el proceso que está realizando. Además, sólo preguntando sabrá cuál es el problema del estudiante. Pregunte y escuche activamente para plantear la siguiente pregunta. |
 |
Es muy probable que nuestros estudiantes busquen en el tutor una respuesta a un problema y tal vez se vayan felices si él les da una. El problema con ello es que no han aprendido cómo llegar a la respuesta y eso es precisamente lo que queremos de ellos: Que aprendan a resolver problemas. |